|
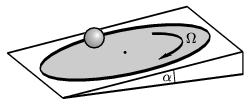
1. feladat. Egy sík, érdes felületű, a vízszinteshez képest
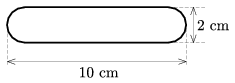
1. ábra Adjunk fizikai magyarázatot a furcsa jelenségre! Milyen irányban és milyen kezdőfeltételekkel kell indítania a bűvésznek a labdát, hogy a mutatvány sikerüljön? (Vigh Máté) 2. feladat. Egy 10 cm hosszú és 2 cm vastag, hengeres üvegrúd mindkét domború vége egy-egy félgömb. A rúd tengelye mentén, egyik végétől mekkora távolságra helyezzünk el egy pontszerű fényforrást a levegőben, ha azt akarjuk, hogy a rúd másik végétől a) ugyanakkora, b) kétszer akkora távolságra találkozzanak az onnan kilépő, a tengellyel kis szöget bezáró fénysugarak? Az üveg levegőre vonatkoztatott törésmutatója 1,5.
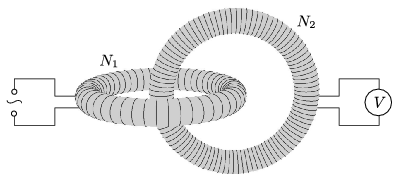
2. ábra (Radnai Gyula) 3. feladat. Két ugyanolyan méretű, csak a menetszámukban különböző, egyenletes tekercselésű, N1 és N2 (>N1) menetes toroid tekercs egymásba van fűzve az ábra szerint. (A középkörök síkjai merőlegesek egymásra.) a) Melyik tekercs kivezetései között indukálódik nagyobb feszültség, ha a másik tekercsben adott effektív áramerősségű és frekvenciájú váltakozó áram folyik? b) Az N1 menetes tekercsre Ueff effektív értékű, hálózati váltakozó feszültséget kapcsolunk, a másik (N2 menetes) tekercs kivezetéseire pedig ideálisnak tekinthető voltmérőt kötünk. Mekkora effektív feszültséget jelez a műszer? Legyen mondjuk N1=100, N2=900, Ueff=230 V!
8. ábra (Vigh Máté) |
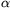 szögben döntött korong egyenletesen,
szögben döntött korong egyenletesen, 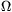 szögsebességgel forog. Egy bűvész a forgó korong közepére egy R sugarú,
tömör gumilabdát helyez, majd megfelelő irányban elgurítja.
A közönség legnagyobb ámulatára a labda középpontja ezután
egyenes vonalú, egyenletes mozgást végez, amit mindaddig folytat, amíg
a labda a forgó korong peremére ér. (A labda
mindvégig tisztán gördül, a korong szögsebessége nem változik.)
szögsebességgel forog. Egy bűvész a forgó korong közepére egy R sugarú,
tömör gumilabdát helyez, majd megfelelő irányban elgurítja.
A közönség legnagyobb ámulatára a labda középpontja ezután
egyenes vonalú, egyenletes mozgást végez, amit mindaddig folytat, amíg
a labda a forgó korong peremére ér. (A labda
mindvégig tisztán gördül, a korong szögsebessége nem változik.)